Pengertian, Contoh Soal Sistem Persamaan Campuran Linear dan Kuadrat

Kompetensi dasar :

Menyelesaikan sistem persamaan linear dan sistem persamaan campuran linear dan kuadrat dua variable.
Merancang model matematika dari masalah yang berkaitan dengan sistem persamaan linear.
Menyelesaikan model matematika dari masalah yang berkaitan dengan sistem persamaan linear dan penafsirannya.

Inti materi:

Sistem persamaan linear dua variable.
Sistem persamaan linear tiga variable.
Aplikasi sistem persamaan linear dua variable dan tiga variable.
Sistem persamaan campuran linear dan kuadrat.

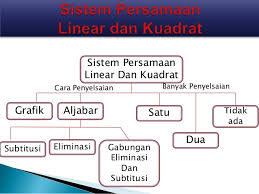
Sistem Persamaan Linear Dan Kuadrat

Sistem Persamaan Linear Dua Variable
Pengertian Sistem Persamaan Linear Dua Variable

Bentuk umum persamaan linear dua variable (PLDV) dengan variable x dan y dapat dinyatakan sebagai berikut:

ax + by = c dengan a, b dan c € R

Defenisi:

Sistem persamaan linear dua variable (PLDV) adalah sistem persamaan yang mempunyai bentuk sebagai berikut.

a1 x + b1 y = c1

a2 x + b2 y = c2

dengan a1, a2, b1, b2, dan c1, c2 adalah bilangan real.

Penyelesaian Sistem Persamaan Linear Dua Variable

Pasangan nilai x dan y yang memenuhi persamaan a x + b y = c dinamakan sebagai penyelesaian dari persamaan tersebut. Untuk menentukan himpunan penyelesaian dari sistem persamaan linear dapat digunakan beberapa cara yaitu:

Menyelesaikan Sistem Persamaan Linear Dua Variable dengan Metode Grafik

Untuk menentukan penyelesaian sistem persamaan linear dua variable a1 x + b1 y = c1 dan a2 x + b2 y = c2 dengan grafik digunakan langkah berikut:

Menggambar garis lurus dari kedua persamaan tersebut pada bidang Cartesius.
Titik potong dari kedua persamaan tersebut merupakan penyelesaian dari sistem persamaan linear.

Contoh: Tentukan himpunan penyelesaian persamaan 2x + 3y = 6 dan 2x + y = -2 dengan metode grafik!

Jawab:

Pada persamaan 2x + 3y = 6

Untuk x = 0 → y = 2

y = 0 → x = 3

Jadi, grafik 2x + 3y = 6 melalui titik (0,2) dan (3,0)

Pada persamaan 2x + y = -2

Untuk x = 0 → y = -2

y = 0 → x = -1

Jadi, grafik 2x + y = -2 melalui titik (0,-2) dan (-1,0)

Dari gambar kita dapat kedua garis lurus dari kedua persamaan berpotongan di satu titik, yaitu (-3,4) Dengan demikian diperoleh himpunan penyelesaiannya adalah (-3,4).

Menyelesaikan Sistem Persamaan Linear Dua Variable dengan Metode Eliminasi

Untuk menentukan penyelesaian sistem persamaan linear dengan metode eliminasi digunakan langkah-langkah sebagai berikut:

Menyamakan koefisien dari variable yang akan dihilangkan dengan cara mengalikan kedua sistem persamaan dengan bilangan yang sesuai.

Melakukan operasi penjumlahan atau pengurangan untuk menghilangkan salah satu variable.

Contoh:

Tentukan himpunan penyelesaian dari sistem persamaan linear x + 3y = 1 dan 2x – y = 9 dengan metode eliminasi!

Jawab:

x + 3y = 1 dikalikan 1 menjadi x + 3y = 1

2x – y = 9 dikalikan 3 menjadi 6x – 3y = 27

7x = 28

x = 4

x + 3y = 1 dikalikan 2 menjadi 2x + 6y = 2

2x – y = 9 dikalikan 1 menjadi 2x – y = 9

7y = -7

y = -1

Jadi, himpunan penyelesaiannya adalah (4,-1)

Menyelesaikan Sistem Persamaan Linear Dua Variable dengan Metode Substitusi

Metode substitusi berarti menggantikan atau menyatakan salah satu variable dalam variable yang lain. Untuk menyelesaikan sistem persamaan linear dua variable dengan metode substitusi digunakan langkah-langkah berikut:

Mengubah salah satu variable menjadi fungsi terhadap variable lainnya pada salah satu persamaan.

Variable yang sudah menjadi fungsi disubstitusi ke persamaan lainnya.

Contoh:

Tentukan himpunan penyelesaian dari sistem persamaan 2x – 3y = -7 dan 3x + 5y = -1 dengan metode substitusi!

Jawab:

2x – 3y = -7 → 3y = 2x + 7

y =

Bentuk y = kemudian disubstitusikan ke dalam persamaan 3x + 5y = -1, sehingga diperoleh 3x + 5 () = -1 ↔ 3x + = -1

↔ 9x + 10x + 35 = -3 ↔ 19x = – 38 ↔ x = -2

Nilai x = -2 disubstitusikan ke dalam y = , sehingga diperoleh y = = 1

Jadi himpunan penyelesaiannya adalah {(-2,1)}.

Menyelesaikan Sistem Persamaan Linear Dua Variable dengan Metode Gabungan Eliminasi dan Substitusi

Metode ini dilakukan dengan cara mengeliminasikan salah satu variable kemudian dilanjutkan dengan mensubstitusikan hasil dari eliminasi tersebut. Metode ini di pandang sebagai metode yang paling efisien digunakan dalam penyelesaian sistem persamaan linear.

Contoh:

Tentukan himpunan penyelesaian dari sistem persamaan 3x + 7y = -1 dan x – 3y = 5 dengan metode gabungan eliminasi dan substitusi!

Jawab:

3x + 7y = -1 dikalikan 1 menjadi 3x + 7y = -1

x – 3y = 5 dikalikan 3 menjadi 3x – 9y = 15

16y = -16

y = -1

substitusi nilai y = -1 ke dalam x – 3y = 5, sehingga

x – 3(-1) = 5 sehingga x = 5 – 3 ↔ x = 2

Jadi, himpunan penyelesainnya adalah {(2,-1)}.

Sistem Persamaan Linear Tiga Variable

Bentuk umum persamaan linear dengan tiga variable, x, y dan z dapat dinyatakan dengan sebagai berikut:

ax + by + cz = d dengan a, b, c dan d € R

Sistem persamaan linear dengan tiga variable adalah system persamaan yang mempunyai bentuk sebagai berikut:

a1 x + b1y + c1z = d1

a2 x + b2y + c2z = d2

a3 x + b3y + c3z = d3

dengan a1, a2, a3, b1, b2, b3, c1, c2, c3, d1, d2 dan d3 adalah bilangan real.

Penyelesaian sistem persamaan dengan tiga variable dapat dilakukan dengan cara yang sama seperti sistem persamaan dengan dua variable. Namun untuk sistem persamaan ini, kita akan gunakan cara yang paling mudah dilakukan, yaitu dengan metode gabungan eliminasi dan substitusi.

Aplikasi Sistem Persamaan Linear Dua Variable dan Tiga Variable

Banyak permasalahan dalam keseharian yang dapat diselesaikan dengan menggunakan bentuk sistem persamaan linear. Dalam hal ini, kita dituntut untuk dapat menerjemahkan soal-soal berupa soal cerita atau informasi ilmiah ke dalam model matematika yang berbentuk sistem persamaan linear dua variable atau tiga variable.

Contoh:

Buk Ani pergi ke pasar untuk membeli sayur-sayuran. Buk Ani membeli tomat 2 kg dan 3 wortel kg lalu membayarnya sebesar Rp. 10.250,00. Dan Anggun juga membeli tomat 3 kg dan 1 kg wortel dengan harga keduanya Rp. 9. 250,00. Jika Ayu juga ingin membeli tomat 1 kg dan wortel 1 kg dengan uang Rp. 10.000,00 maka berapakah kembalian uang Ayu?

Jawab:

Misalnya, harga 1 kg tomat = x rupiah

Harga 1 kg wortel = y rupiah

Maka diperoleh sistem persamaan

2x + 3y = Rp. 10.250,00 …… (1)

3x + y = Rp. 9,250,00 ……..( 2)

Eliminasi persamaan

2x + 3y = Rp. 10.250,00 dikalikan 3 menjadi ↔ 6x + 9y = 30.750

3x + y = Rp. 9,250,00 dikalikan 2 menjadi ↔ 6x + 2y = 18.500

7y = 12.250

y = 1.750 ….(3)

Substitusi persamaan (3)ke persamaan (1), sehingga di peroleh

2x + 3y = Rp. 10.250

↔ 2x + 3(1.750) = 10.250

↔ 2x = 5.000

↔ x = 2.500

Jadi, uang kembalian yang diterima Ayu adalah

= Rp. 10.000 – ( x+ y)

= Rp. 10.000 – ( 2.500 + 1.750)

= Rp. 5. 750,00

Sistem Persamaan Campuran Linear dan Kuadrat

Defenisi

Bentuk umum persamaan campuran linear dan kuadrat dapat dinyatakan sebagai berikut:

y = ax + b

y = px2 + qx +r

dengan a, b, p, q dan r adalah bilangan-bilangan real, a ≠ 0 dan p ≠ 0

Untuk menyelesaikan sistem persamaan campuran linear dan kuadrat dapat digunakan metode subtitusi. Dengan mensubstitusi persamaan linear y = ax + b ke persamaan kuadrat

y = px2 + qx +r, maka

ax + b = px2 + qx + r

px2 + qx – ax + r – b = 0

px2 + (q – a)x + r – b = 0

Persamaan px2 + (q – a)x + r – b = 0 merupakan persamaan kuadrat yang mempunyai nilai Diskriminan D = (q – a)2 – 4 p(r – b).

Banyaknya anggota himpunan penyelesaian ditentukan oleh nilai diskriminan tersebut.

Jika D > 0, maka sistem persamaan campuran linear dan kuadrat mempunyai dua anggota dalam himpunan penyelesaian.

Jika D = 0, maka persamaan campuran linear dan kuadrat mempunyai satu anggota dalam himpunan penyelesaian.

Jika D < 0, persamaan campuran linear dan kuadrat tidak mempunyai anggota dalam himpunan penyelesaian atau {}.

Contoh:

Tentukan impunan penyelesaian dari sistem persamaan 2x – y = 2 dan y = x2 + 5x – 6?

Jawab:

2x – y = 2 → y= 2x – 2….(1)

y = x2 + 5x – 6 ….(2)

Substitusikan persamaan (1) dan (2) sehingga di peroleh

2x – 2 = x2 + 5x – 6

↔ x2 + 5x – 2x – 6 + 2 = 0

↔ x2 + 3x – 4 = 0

↔ (x – 1) (x + 4) = 0

x1 = 1 atau x2 = -4

untuk x1 = 1 → y1 = 2(1) – 2 = 0

x2 = -4 → y2 = 2(-4) – 2 = -10

Jadi, himpunan penyelesainnya adalah {(1,0), (-4,-10)}

Sumber : Anikeputri